下図: ダウンフォースを発生するウイングの例。
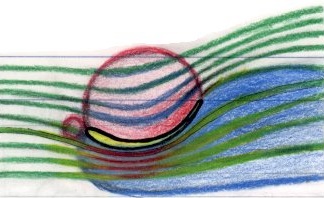
赤い空間が高圧で、青い空間が低圧である。
もっと正確に云うと、車輌は地面より上方で走行している事で、空気抵抗となる物体にはモーメントが作用する為、
その物体の抗力(=空気抵抗)もダウンフォースとして作用する。だがそれはあまり大きな値ではない。
例えば、レーシングカーのリヤ・ウイングは、高く、後方へ設置する程、テコの原理でダウンフォースが増加する。
では、次は気流の仕組みについて考察していこう。
下図: ダウンフォースを発生するウイングの例。

赤い空間が高圧で、青い空間が低圧である。
気流進路の色は、赤が高速、緑が中速、青が低速である。
つまり、流速が増せば圧力が低下し、流速が減少すれば圧力は高まる。
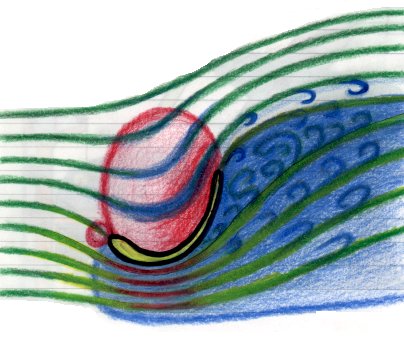
しかし、より大きなダウンフォースを得ようとしてウイングの角度を大きく立て過ぎると、
ウイング上面の圧力は増すのだが、
ウイング下面の気流は、粘性の影響で「剥離」してしまう。
気流が剥離すると、ダウンフォースが激減してしまう。
空気の粘性によるブレーキ効果ともう一つ、ここで流れが剥離する理由は、
流れの方向へ圧力が高まってゆくという事が挙げられる。
ウイングの断面積が最大になる地点で、最も流速が高くなるが、
そこから後方へは流速が低下してゆく事を意味し、
流速が低下すれば、そのエリアの圧力は高くなってゆく。
流体は圧力の高い所から低い所へ流れるので、
流れの方向へ圧力が高まってゆくと流れ辛く、流れが剥離する訳だ。
つまり、気流が剥離すると、ウイング下面の「後ろ側の流れが滞り、」
ウイング後方の低圧による吸い出し量が減少してしまう。
この状態では、ウイング下面ではあまりダウンフォースが発生できず、空力効率が悪い。
そこで、効率良く、大きなダウンフォースを得られる方法が、下図の間隙フラップだ。
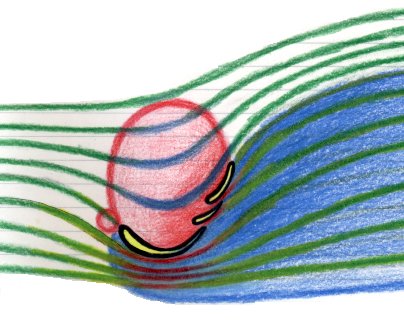
これはウイングの途中に隙間を開け、
フラップ下側の気流が剥離する手前の箇所に、
(つまり運動エネルギーを失いかけた気流へ、)
フラップ下面へ運動エネルギーの強い気流を噴き出す事で、
フラップ下側の気流(=粘性がある)を加速させ、剥離を防いでいる。
これで大きな向かえ角度でもウイング下面の気流を剥離させず、
大きなダウンフォースを発生できる。
ウイング(翼)の揚力発生の原理は、諸説別れるが、基本的にはベルヌーイの定理(Bernoulli's principle)から説明できる。
これはダニエル・ベルヌーイ氏(Daniel Bernoulli 1700〜1782)によって 1738年に発表されたとされている。
これは、流れに沿って成り立つエネルギー保存の法則で、流体の挙動を平易に表した式である。
これを簡単に述べてしまうと、「(完全流体においては,) 流速と圧力と位置エネルギーの和は不変である」と云えると思う。
(これは筆者による和訳・記述概念だ。概要は一応合っていると思う。)
完全流体と云うのは、流体力学を簡単に思考する為の仮想の流体で、粘性(=摩擦)の無い仮想の流体概念である。
つまり、実際の流体の事象を考察するにあたっては、ベルヌーイの定理に加えて、流体が受ける粘性を考慮する必要があると云う事だ。
ベルヌーイの定理を超簡単に述べると、(流速が音速未満で,開かれた空間にては,) 流体は、
流速が上がると圧力は低下し、
流速が下がると圧力は高くなる。 (=事象としてこの事実は確認されている。)
位置エネルギーとは、
例えば野球のボールを1メートルの高さからアスファルトの地面へ落としてみると、
ボールが持っている運動エネルギーによる反発力から、ボールは少し跳ね上がる。
では、同じボールを、百メートルの高さから落としてみると、落下し着地した際のGフォース(重力加速度)はとても大きくなる。
これはボールが持っていた位置エネルギーが運動エネルギーへ変わった結果である。(なので着地で大きなGフォースが発生する。)
位置エネルギーの概念は、やや解り難いかもしれないので、では少し上記とは違う述べ方をしてみよう。
まず、人が平地に居る。そして目の前の山を登ってゆく。やっと頂上に到着し、体力が消耗した。これは運動エネルギーが位置エネルギーへ変わったと云う訳だ。
気流も、登る時も降りる時も、エネルギーを消費するのだ。
最高速400km/h以下の自動車レースの世界では、圧縮は考慮せずに済み、(ただし閉じられた空間にはラム圧がかかる。)
音速を超える高速航空機やロケットの世界では、高圧による圧縮を考慮する必要があると云う事である。
(このページの更新日:2015. 5.30土
スマホ用にページ編集加筆:2019. 5.17金)